[프로그래머스] 미로 탈출 / 2021 카카오 채용연계형 인턴십 - JAVA

🖇️ 문제 링크

코딩테스트 연습 - 미로 탈출

신규 게임 '카카오 미로 탈출'이 출시되어, 라이언 이 베타테스터로 참가했습니다. 위 예시 그림은 카카오 미로 탈출의 초기 상태를 나타냅니다. 1번부터 3번까지 번호가 붙어있는 3개의 방이 있고, 방과 방 사이를 연결하는 길에는 이동하는데 걸리는 시간이 표시되어 있습니다. 길은 화살표가 가리키는 방향으로만 이동할 수 있습니다. 미로에는 함정이 존재하며, 함정으로 이동하면, 이동한 함정과 연결된 모든 화살표의 방향이 바뀝니다.

https://programmers.co.kr/learn/courses/30/lessons/81304

 

---

📝 문제 분석

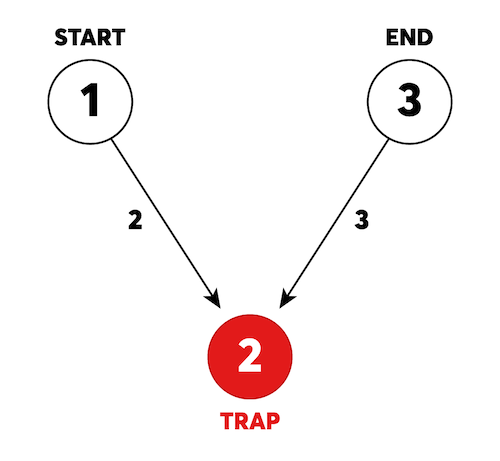
평범한 다익스트라 문제에 트랩이라는 매커니즘을 적용시켜야 하는 문제입니다.

트랩은 최대 10개가 있을 수 있기 때문에 2^10, 총 1024개의 그래프가 나올 수 있습니다.

이를 모두 저장하고 있을 수는 없기 때문에, 트랩들의 인덱스를 비트로 표현하여 저장합니다,

 

// 다익스트라, 다음 노드를 찾는 과정
for(Edge next : adj[curNode]) {
    int nextNode = next.to;
    int nextCost = next.cost;
    int isReverse = next.state;

    if(isReverse != (isConnected(curNode, nextNode, curState, trap) ? 1 : 0))
        continue;

    int nextState = getNextState(curState, nextNode, trap);
    nextCost += curCost;

    if(nextCost >= dist[nextNode][nextState])
        continue;

    dist[nextNode][nextState] = nextCost;
    pq.add(new Edge(nextNode, nextCost, nextState));
}

현재 노드와 다음 노드의 상태에 따라 그래프의 형태가 달라지게 됩니다.

1. 현재 노드, 다음 노드 둘다 트랩이 아닐 때 or 둘 다 트랩이고 활성화 상태일 때 : 원래 그래프 그대로 사용

2. 둘 중 하나만 트랩이고 활성화 상태일 때 : 거꾸로 된 그래프 사용

 

int[][] dist = new int[n + 1][1 << 10];

최단 거리를 찾는 배열도 현재 그래프 상태를 고려해서 계산해야하기 때문에 dist[정점 번호][그래프 상태] 형태로 구현합니다.

 

---

⌨️ 코드

import java.util.*;

class Solution {
    public int solution(int n, int start, int end, int[][] roads, int[] traps) {
        List<Edge>[] adj = new ArrayList[n + 1];
        Map<Integer, Integer> trap = new HashMap<>();
        int ans = (int)1e9;

        for(int i = 1; i <= n; i++)
            adj[i] = new ArrayList<>();

        for(int[] road : roads) {
            adj[road[0]].add(new Edge(road[1], road[2], 0));
            adj[road[1]].add(new Edge(road[0], road[2], 1));
        }

        for(int i = 0; i < traps.length; i++)
            trap.put(traps[i], i);

        // 다익스트라
        int[][] dist = new int[n + 1][1 << 10];
        for(int i = 1; i <= n; i++)
            Arrays.fill(dist[i], (int)1e9);

        PriorityQueue<Edge> pq = new PriorityQueue<>();
        pq.add(new Edge(start, 0, 0));
        dist[start][0] = 0;

        while(!pq.isEmpty()) {
            Edge cur = pq.poll();
            int curNode = cur.to;
            int curCost = cur.cost;
            int curState = cur.state;

            // end에 도착했을 때
            if(curNode == end) {
                ans = Math.min(ans, curCost);
                continue;
            }

            if(curCost > dist[curNode][curState])
                continue;

            for(Edge next : adj[curNode]) {
                int nextNode = next.to;
                int nextCost = next.cost;
                int isReverse = next.state;

                if(isReverse != (isConnected(curNode, nextNode, curState, trap) ? 1 : 0))
                    continue;

                int nextState = getNextState(curState, nextNode, trap);
                nextCost += curCost;

                if(nextCost >= dist[nextNode][nextState])
                    continue;

                dist[nextNode][nextState] = nextCost;
                pq.add(new Edge(nextNode, nextCost, nextState));
            }
        }

        return ans;
    }

    public int getNextState(int curState, int nextNode, Map<Integer, Integer> trap) {
        if(trap.containsKey(nextNode))
            curState ^= (1 << trap.get(nextNode));
        return curState;
    }


    public boolean isConnected(int curNode, int nextNode, int curState, Map<Integer, Integer> trap) {
        boolean currNodeTrapChk = false, nextNodeTrapChk = false;

        if(trap.containsKey(curNode))
            currNodeTrapChk = ((curState & (1 << trap.get(curNode))) != 0);

        if(trap.containsKey(nextNode))
            nextNodeTrapChk = ((curState & (1 << trap.get(nextNode))) != 0);

        return currNodeTrapChk ^ nextNodeTrapChk;
    }

    class Edge implements Comparable<Edge> {
        int to, cost, state;

        Edge(int to, int cost, int state) {
            this.to = to;
            this.cost = cost;
            this.state = state;
        }

        @Override
        public int compareTo(Edge o) {
            return this.cost - o.cost;
        }
    }

}

 

 

 

 

Uploaded by Notion2Tistory v1.1.0